|
|
Lists are probably the most commonly used data structure in Scala programs. This chapter explains lists in detail. It presents many common operations that can be performed on lists. It also teaches some important design principles for programs working on lists.
You saw lists already in the preceding chapters, so you know that a list containing the elements 'a', 'b', and 'c' is written List('a', 'b', 'c'). Here are some other examples:
val fruit = List("apples", "oranges", "pears") val nums = List(1, 2, 3, 4) val diag3 = List( List(1, 0, 0), List(0, 1, 0), List(0, 0, 1) ) val empty = List()Lists are quite similar to arrays, but there are two important differences. First, lists are immutable. That is, elements of a list cannot be changed by assignment. Second, lists have a recursive structure (i.e., a linked list),[1] whereas arrays are flat.
Like arrays, lists are homogeneous: the elements of a list all have the same type. The type of a list that has elements of type T is written List[T]. For instance, here are the same four lists with explicit types added:
val fruit: List[String] = List("apples", "oranges", "pears") val nums: List[Int] = List(1, 2, 3, 4) val diag3: List[List[Int]] = List( List(1, 0, 0), List(0, 1, 0), List(0, 0, 1) ) val empty: List[Nothing] = List()
The list type in Scala is covariant. This means that for each pair of types S and T, if S is a subtype of T, then List[S] is a subtype of List[T]. For instance, List[String] is a subtype of List[Object]. This is natural because every list of strings can also be seen as a list of objects.[2]
Note that the empty list has type List[Nothing]. You saw in Section 11.3 that Nothing is the bottom type in Scala's class hierarchy. It is a subtype of every other Scala type. Because lists are covariant, it follows that List[Nothing] is a subtype of List[T], for any type T. So the empty list object, which has type List[Nothing], can also be seen as an object of every other list type of the form List[T]. That's why it is permissible to write code like:
// List() is also of type List[String]! val xs: List[String] = List()
All lists are built from two fundamental building blocks, Nil and :: (pronounced "cons"). Nil represents the empty list. The infix operator, ::, expresses list extension at the front. That is, x :: xs represents a list whose first element is x, followed by (the elements of) list xs. Hence, the previous list values could also have been defined as follows:
val fruit = "apples" :: ("oranges" :: ("pears" :: Nil)) val nums = 1 :: (2 :: (3 :: (4 :: Nil))) val diag3 = (1 :: (0 :: (0 :: Nil))) :: (0 :: (1 :: (0 :: Nil))) :: (0 :: (0 :: (1 :: Nil))) :: Nil val empty = NilIn fact the previous definitions of fruit, nums, diag3, and empty in terms of List(...) are just wrappers that expand to these definitions. For instance, List(1, 2, 3) creates the list 1 :: (2 :: (3 :: Nil)).
Because it ends in a colon, the :: operation associates to the right: A :: B :: C is interpreted as A :: (B :: C). Therefore, you can drop the parentheses in the previous definitions. For instance:
val nums = 1 :: 2 :: 3 :: 4 :: Nilis equivalent to the previous definition of nums.
All operations on lists can be expressed in terms of the following three:
| head | returns the first element of a list |
| tail | returns a list consisting of all elements except the first |
| isEmpty | returns true if the list is empty |
These operations are defined as methods of class List. Some examples are shown in Table 16.1.
| What it is | What it does |
| empty.isEmpty | returns true |
| fruit.isEmpty | returns false |
| fruit.head | returns "apples" |
| fruit.tail.head | returns "oranges" |
| diag3.head | returns List(1, 0, 0) |
The head and tail methods are defined only for non-empty lists. When selected from an empty list, they throw an exception. For instance:
scala> Nil.head
java.util.NoSuchElementException: head of empty list
As an example of how lists can be processed, consider sorting the
elements of a list of numbers into ascending order. One simple way to
do so is insertion sort, which works as follows: To sort a
non-empty list x :: xs, sort
the remainder xs and insert the first element x at the right
position in the result. Sorting an empty list yields the
empty list. Expressed as Scala code, the insertion sort algorithm looks like:
def isort(xs: List[Int]): List[Int] = if (xs.isEmpty) Nil else insert(xs.head, isort(xs.tail))
def insert(x: Int, xs: List[Int]): List[Int] = if (xs.isEmpty || x <= xs.head) x :: xs else xs.head :: insert(x, xs.tail)
Lists can also be taken apart using pattern matching. List patterns correspond one-by-one to list expressions. You can either match on all elements of a list using a pattern of the form List(...), or you take lists apart bit by bit using patterns composed from the :: operator and the Nil constant.
Here's an example of the first kind of pattern:
scala> val List(a, b, c) = fruit a: String = apples b: String = oranges c: String = pearsThe pattern List(a, b, c) matches lists of length 3, and binds the three elements to the pattern variables a, b, and c. If you don't know the number of list elements beforehand, it's better to match with :: instead. For instance, the pattern a :: b :: rest matches lists of length 2 or greater:
If you review the possible forms of patterns explained in Chapter 15, you might find that neither List(...) nor :: looks like it fits one of the kinds of patterns defined there. In fact, List(...) is an instance of a library-defined extractor pattern. Such patterns will be treated in Chapter 24. The "cons" pattern x :: xs is a special case of an infix operation pattern. You know already that, when seen as an expression, an infix operation is equivalent to a method call. For patterns, the rules are different: When seen as a pattern, an infix operation such as p op q is equivalent to op(p, q). That is, the infix operator op is treated as a constructor pattern. In particular, a cons pattern such as x :: xs is treated as ::(x, xs). This hints that there should be a class named :: that corresponds to the pattern constructor. Indeed there is such as class. It is named scala.:: and is exactly the class that builds non-empty lists. So :: exists twice in Scala, once as a name of a class in package scala, and again as a method in class List. The effect of the method :: is to produce an instance of the class scala.::. You'll find out more details about how the List class is implemented in Chapter 22.
scala> val a :: b :: rest = fruit a: String = apples b: String = oranges rest: List[String] = List(pears)Taking lists apart with patterns is an alternative to taking them apart with the basic methods head, tail, and isEmpty. For instance, here's insertion sort again, this time written with pattern matching:
def isort(xs: List[Int]): List[Int] = xs match { case List() => List() case x :: xs1 => insert(x, isort(xs1)) }
def insert(x: Int, xs: List[Int]): List[Int] = xs match { case List() => List(x) case y :: ys => if (x <= y) x :: xs else y :: insert(x, ys) }
Often, pattern matching over lists is clearer than decomposing them with methods, so pattern matching should be a part of your list processing toolbox.
This is all you need to know about lists in Scala to be able to use them correctly. However, there are also a large number of methods that capture common patterns of operations over lists. These methods make list processing programs more concise and often clearer. The next two sections present the most important methods defined in the List class.
This section explains most first-order methods defined in the List class. A method is first-order if it does not take any functions as arguments. The section also introduces by means of two examples some recommended techniques to structure programs that operate on lists.
An operation similar to :: is list concatenation, written `:::'. Unlike ::, ::: takes two lists as operands. The result of xs ::: ys is a new list that contains all the elements of xs, followed by all the elements of ys. Here are some examples:
scala> List(1, 2) ::: List(3, 4, 5) res0: List[Int] = List(1, 2, 3, 4, 5)Like cons, list concatenation associates to the right. An expression like this:
scala> List() ::: List(1, 2, 3) res1: List[Int] = List(1, 2, 3)
scala> List(1, 2, 3) ::: List(4) res2: List[Int] = List(1, 2, 3, 4)
xs ::: ys ::: zsis interpreted like this:
xs ::: (ys ::: zs)
Concatenation (:::) is implemented as a method in class List. It would also be possible to implement concatenation "by hand," using pattern matching on lists. It's instructive to try to do that yourself, because it shows a common way to implement algorithms using lists. First, we'll settle on a signature for the concatenation method, which we'll call append. In order not to mix things up too much, assume that append is defined outside the List class. So it will take the two lists to be concatenated as parameters. These two lists must agree on their element type, but that element type can be arbitrary. This can be expressed by giving append a type parameter[3] that represents the element type of the two input lists:
def append[T](xs: List[T], ys: List[T]): List[T]To design the implementation of append, it pays to remember the "divide and conquer" design principle for programs over recursive data structures such as lists. Many algorithms over lists first split an input list into simpler cases using a pattern match. That's the divide part of the principle. They then construct a result for each case. If the result is a non-empty list, some of its parts may be constructed by recursive invocations of the same algorithm. That's the conquer part of the principle.
To apply this principle to the implementation of the append method, the first question to ask is on which list to match. This is less trivial in the case of append than for many other methods because there are two choices. However, the subsequent "conquer" phase tells you that you need to construct a list consisting of all elements of both input lists. Since lists are constructed from the back towards the front, ys can remain intact whereas xs will need to be taken apart and prepended to ys. Thus, it makes sense to concentrate on xs as a source for a pattern match. The most common pattern match over lists simply distinguishes an empty from a non-empty list. So this gives the following outline of an append method:
def append[T](xs: List[T], ys: List[T]): List[T] = xs match { case List() => // ?? case x :: xs1 => // ?? }All that remains is to fill in the two places marked with "??". The first such place is the alternative where the input list xs is empty. In this case concatenation yields the second list:
case List() => ysThe second place left open is the alternative where the input list xs consists of some head x followed by a tail xs1. In this case the result is also a non-empty list. To construct a non-empty list you need to know what the head and the tail of that list should be. You know that the first element of the result list is x. As for the remaining elements, these can be computed by appending the rest of the first list, xs1, to the second list ys. This completes the design and gives:
def append[T](xs: List[T], ys: List[T]): List[T] = xs match { case List() => ys case x :: xs1 => x :: append(xs1, ys) }The computation of the second alternative illustrated the "conquer" part of the divide and conquer principle: Think first what the shape of the desired output should be, then compute the individual parts of that shape, using recursive invocations of the algorithm where appropriate. Finally, construct the output from these parts.
The length method computes the length of a list.
scala> List(1, 2, 3).length res3: Int = 3On lists, unlike arrays, length is a relatively expensive operation. It needs to traverse the whole list to find its end and therefore takes time proportional to the number of elements in the list. That's why it's not a good idea to replace a test such as xs.isEmpty by xs.length == 0. The result of the two tests are equivalent, but the second one is slower, in particular if the list xs is long.
You know already the basic operations head and tail, which respectively take the first element of a list, and the rest of the list except the first element. They each have a dual operation: last returns the last element of a (non-empty) list, whereas init returns a list consisting of all elements except the last one:
scala> val abcde = List('a', 'b', 'c', 'd', 'e') abcde: List[Char] = List(a, b, c, d, e)Like head and tail, these methods throw an exception when applied to an empty list:
scala> abcde.last res4: Char = e
scala> abcde.init res5: List[Char] = List(a, b, c, d)
scala> List().init java.lang.UnsupportedOperationException: Nil.init at scala.List.init(List.scala:544) at ...Unlike head and tail, which both run in constant time, init and last need to traverse the whole list to compute their result. They therefore take time proportional to the length of the list.
scala> List().last java.util.NoSuchElementException: Nil.last at scala.List.last(List.scala:563) at ...
It's a good idea to organize your data so that
most accesses are at the head of a list, rather than the last element.
If at some point in the computation an algorithm demands frequent accesses to the end of a list, it's sometimes better to reverse the list first and work with the result instead. Here's how to do the reversal:
scala> abcde.reverse
res6: List[Char] = List(e, d, c, b, a)
Note that, like all other list operations, reverse creates a new
list rather than changing the one it operates on. Since lists are
immutable, such a change would not be possible, anyway. To verify
this, check that the original value of abcde is unchanged after the
reverse operation:
scala> abcde
res7: List[Char] = List(a, b, c, d, e)
The reverse, init, and last operations satisfy some
laws which can be used for reasoning about computations and for
simplifying programs.
xs.reverse.reverse equals xs
xs.reverse.init equals xs.tail.reverse xs.reverse.tail equals xs.init.reverse xs.reverse.head equals xs.last xs.reverse.last equals xs.head
def rev[T](xs: List[T]): List[T] = xs match { case List() => xs case x :: xs1 => rev(xs1) ::: List(x) }However, this method is less efficient than one would hope for. To study the complexity of rev, assume that the list xs has length n. Notice that there are n recursive calls to rev. Each call except the last involves a list concatenation. List concatenation xs ::: ys takes time proportional to the length of its first argument xs. Hence, the total complexity of rev is:
In other words, rev's complexity is quadratic in the length of its input argument. This is disappointing when compared to the standard reversal of a mutable, linked list, which has linear complexity. However, the current implementation of rev is not the best implementation possible. You will see in Section 16.7 how to speed it up.
The drop and take operations generalize tail and init in that they return arbitrary prefixes or suffixes of a list. The expression "xs take n" returns the first n elements of the list xs. If n is greater than xs.length, the whole list xs is returned. The operation "xs drop n" returns all elements of the list xs except the first n ones. If n is greater than xs.length, the empty list is returned.
The splitAt operation splits the list at a given index, returning a pair of two lists.[4] It is defined by the equality:
However, splitAt avoids traversing the list xs twice. Here are some examples of these three methods:
scala> abcde take 2 res8: List[Char] = List(a, b)
scala> abcde drop 2 res9: List[Char] = List(c, d, e)
scala> abcde splitAt 2 res10: (List[Char], List[Char]) = (List(a, b),List(c, d, e))
Random element selection is supported through the apply method; however it is a less common operation for lists than it is for arrays.
scala> abcde apply 2 // rare in Scala res11: Char = cAs for all other types, apply is implicitly inserted when an object appears in the function position in a method call, so the line above can be shortened to:
scala> abcde(2) // rare in Scala res12: Char = cOne reason why random element selection is less popular for lists than for arrays is that xs(n) takes time proportional to the index n. In fact, apply is simply defined by a combination of drop and head:
This definition also makes clear that list indices range from 0 up to the length of the list minus one, the same as for arrays. The indices method returns a list consisting of all valid indices of a given list:
scala> abcde.indices
res13: List[Int] = List(0, 1, 2, 3, 4)
The zip operation takes two lists and forms a list of pairs:
scala> abcde.indices zip abcde res14: List[(Int, Char)] = List((0,a), (1,b), (2,c), (3,d), (4,e))If the two lists are of different length, any unmatched elements are dropped:
scala> val zipped = abcde zip List(1, 2, 3) zipped: List[(Char, Int)] = List((a,1), (b,2), (c,3))A useful special case is to zip a list with its index. This is done most efficiently with the zipWithIndex method, which pairs every element of a list with the position where it appears in the list.
scala> abcde.zipWithIndex res15: List[(Char, Int)] = List((a,0), (b,1), (c,2), (d,3), (e,4))
The toString operation returns the canonical string representation of a list:
scala> abcde.toString
res16: String = List(a, b, c, d, e)
If you want a different representation you can use the mkString
method. The operation xs mkString (pre, sep, post) involves four
operands:
the list xs to be displayed, a prefix string pre to be
displayed in front of all elements, a separator string sep to be displayed
between successive elements, and a postfix string post to be
displayed at the end. The result of the operation is the string:
The mkString method has two overloaded variants that let you drop some or all of its arguments. The first variant only takes a separator string:
The second variant lets you omit all arguments:
Here are some examples:
scala> abcde mkString ("[", ",", "]") res17: String = [a,b,c,d,e]There are also variants of the mkString methods called addString which append the constructed string to a StringBuilder object,[5] rather than returning them as a result:
scala> abcde mkString "" res18: String = abcde
scala> abcde.mkString res19: String = abcde
scala> abcde mkString ("List(", ", ", ")") res20: String = List(a, b, c, d, e)
scala> val buf = new StringBuilder buf: StringBuilder =The mkString and addString methods are inherited from List's super trait Iterable, so they are applicable to all sorts of iterable collections.
scala> abcde addString (buf, "(", ";", ")") res21: StringBuilder = (a;b;c;d;e)
To convert data between the flat world of arrays and the recursive world of lists, you can use method toArray in class List and toList in class Array:
scala> val arr = abcde.toArray arr: Array[Char] = Array(a, b, c, d, e)There's also a method copyToArray, which copies list elements to successive array positions within some destination array. The operation:
scala> arr.toString res22: String = Array(a, b, c, d, e)
scala> arr.toList res23: List[Char] = List(a, b, c, d, e)
xs copyToArray (arr, start)copies all elements of the list xs to the array arr, beginning with position start. You must ensure that the destination array arr is large enough to hold the list in full. Here's an example:
scala> val arr2 = new Array[Int](10) arr2: Array[Int] = Array(0, 0, 0, 0, 0, 0, 0, 0, 0, 0)Finally, if you need to access list elements via an iterator, you can use the elements method:
scala> List(1, 2, 3) copyToArray (arr2, 3)
scala> arr2.toString res25: String = Array(0, 0, 0, 1, 2, 3, 0, 0, 0, 0)
scala> val it = abcde.elements it: Iterator[Char] = non-empty iterator
scala> it.next res26: Char = a
scala> it.next res27: Char = b
The insertion sort presented earlier is concise to write, but it is not very efficient. Its average complexity is proportional to the square of the length of the input list. A more efficient algorithm is merge sort.
This example provides another illustration of the divide and conquer principle and currying, as well as a useful discussion of algorithmic complexity. If you prefer to move a bit faster on your first pass through this book, however, you can safely skip to Section 16.7.
Merge sort works as follows: First, if the list has zero or one elements, it is already sorted, so the list can be returned unchanged. Longer lists are split into two sub-lists, each containing about half the elements of the original list. Each sub-list is sorted by a recursive call to the sort function, and the resulting two sorted lists are then combined in a merge operation.
For a general implementation of merge sort, you want to leave open the type of list elements to be sorted, and also want to leave open the function to be used for the comparison of elements. You obtain a function of maximal generality by passing these two items as parameters. This leads to the implementation shown in Listing 16.1.
def msort[T](less: (T, T) => Boolean) (xs: List[T]): List[T] = {
def merge(xs: List[T], ys: List[T]): List[T] = (xs, ys) match { case (Nil, _) => ys case (_, Nil) => xs case (x :: xs1, y :: ys1) => if (less(x, y)) x :: merge(xs1, ys) else y :: merge(xs, ys1) }
val n = xs.length / 2 if (n == 0) xs else { val (ys, zs) = xs splitAt n merge(msort(less)(ys), msort(less)(zs)) } }
The complexity of msort is order (n\;log(n)), where n is the length of the input list. To see why, note that splitting a list in two and merging two sorted lists each take time proportional to the length of the argument list(s). Each recursive call of msort halves the number of elements in its input, so there are about log(n) consecutive recursive calls until the base case of lists of length 1 is reached. However, for longer lists each call spawns off two further calls. Adding everything up we obtain that at each of the log(n) call levels, every element of the original lists takes part in one split operation and in one merge operation. Hence, every call level has a total cost proportional to n. Since there are log(n) call levels, we obtain an overall cost proportional to n\;log(n). That cost does not depend on the initial distribution of elements in the list, so the worst case cost is the same as the average case cost. This property makes merge sort an attractive algorithm for sorting lists.
Here is an example of how msort is used:
scala> msort((x: Int, y: Int) => x < y)(List(5, 7, 1, 3)) res28: List[Int] = List(1, 3, 5, 7)
The msort function is a classical example of the currying concept discussed in Section 9.3. Currying makes it easy to specialize the function for particular comparison functions. Here's an example:
scala> val intSort = msort((x: Int, y: Int) => x < y) _ intSort: (List[Int]) => List[Int] = <function>The intSort variable refers to a function that takes a list of integers and sorts them in numerical order. As described in Section 8.6, an underscore stands for a missing argument list. In this case, the missing argument is the list that should be sorted. As another example, here's how you could define a function that sorts a list of integers in reverse numerical order:
scala> val reverseIntSort = msort((x: Int, y: Int) => x > y) _ reverseIntSort: (List[Int]) => List[Int] = <function>
Because you provided the comparison function already via currying, you now need only provide the list to sort when you invoke the intSort or reverseIntSort functions. Here are some examples:
scala> val mixedInts = List(4, 1, 9, 0, 5, 8, 3, 6, 2, 7) mixedInts: List[Int] = List(4, 1, 9, 0, 5, 8, 3, 6, 2, 7)
scala> intSort(mixedInts) res0: List[Int] = List(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
scala> reverseIntSort(mixedInts) res1: List[Int] = List(9, 8, 7, 6, 5, 4, 3, 2, 1, 0)
Many operations over lists have a similar structure. Several patterns appear time and time again. Some examples are: transforming every element of a list in some way, verifying whether a property holds for all elements of a list, extracting from a list elements satisfying a certain criterion, or combining the elements of a list using some operator. In Java, such patterns would usually be expressed by idiomatic combinations of for or while loops. In Scala, they can be expressed more concisely and directly using higher-order operators,[6] which are implemented as methods in class List. These higher-order operators are discussed in this section.
The operation xs map f takes as operands a list xs of type List[T] and a function f of type T => U. It returns the list resulting from applying the function f to each list element in xs. For instance:
scala> List(1, 2, 3) map (_ + 1) res29: List[Int] = List(2, 3, 4)The flatMap operator is similar to map, but it takes a function returning a list of elements as its right operand. It applies the function to each list element and returns the concatenation of all function results. The difference between map and flatMap is illustrated in the following example:
scala> val words = List("the", "quick", "brown", "fox") words: List[java.lang.String] = List(the, quick, brown, fox)
scala> words map (_.length) res30: List[Int] = List(3, 5, 5, 3)
scala> words map (_.toList.reverse.mkString) res31: List[String] = List(eht, kciuq, nworb, xof)
scala> words map (_.toList) res32: List[List[Char]] = List(List(t, h, e), List(q, u, i, c, k), List(b, r, o, w, n), List(f, o, x))You see that where map returns a list of lists, flatMap returns a single list in which all element lists are concatenated.
scala> words flatMap (_.toList) res33: List[Char] = List(t, h, e, q, u, i, c, k, b, r, o, w, n, f, o, x)
The differences and interplay between map and flatMap are also demonstrated by the following expression, which constructs a list of all pairs (i, j) such that 1 ≤ j < i < 5:
scala> List.range(1, 5) flatMap ( i => List.range(1, i) map (j => (i, j)) ) res34: List[(Int, Int)] = List((2,1), (3,1), (3,2), (4,1), (4,2), (4,3))List.range is a utility method that creates a list of all integers in some range. It is used twice in this example: once to generate a list of integers from 1 (including) until 5 (excluding), and in a second time to generate a list of integers from 1 until i, for each value of i taken from the first list. The map in this expression generates a list of tuples (i, j) where j < i. The outer flatMap in this example generates this list for each i between 1 and 5, and then concatenates all the results.
Note that the same list can alternatively be constructed with a for expression:
for (i <- List.range(1, 5); j <- List.range(1, i)) yield (i, j)You'll learn more about the interplay of for expressions and list operations in Chapter 23.
The third map-like operation is foreach. Unlike map and flatMap, however, foreach takes a procedure (a function with result type Unit) as right operand. It simply applies the procedure to each list element. The result of the operation itself is again Unit; no list of results is assembled. As an example, here is a concise way of summing up all numbers in a list:
scala> var sum = 0 sum: Int = 0
scala> List(1, 2, 3, 4, 5) foreach (sum += _)
scala> sum res36: Int = 15
The operation "xs filter p" takes as operands a list xs of type List[T] and a predicate function p of type T => Boolean. It yields the list of all elements x in xs for which p(x) is true. For instance:
scala> List(1, 2, 3, 4, 5) filter (_ % 2 == 0) res37: List[Int] = List(2, 4)The partition method is like filter, but it returns a pair of lists. One list contains all elements for which the predicate is true, while the other list contains all elements for which the predicate is false. It is defined by the equality:
scala> words filter (_.length == 3) res38: List[java.lang.String] = List(the, fox)
Here's an example:
scala> List(1, 2, 3, 4, 5) partition (_ % 2 == 0) res39: (List[Int], List[Int]) = (List(2, 4),List(1, 3, 5))The find method is also similar to filter but it returns the first element satisfying a given predicate, rather than all such elements. The operation xs find p takes a list xs and a predicate p as operands. It returns an optional value. If there is an element x in xs for which p(x) is true, Some(x) is returned. Otherwise, p is false for all elements, and None is returned. Here are some examples:
scala> List(1, 2, 3, 4, 5) find (_ % 2 == 0) res40: Option[Int] = Some(2)The takeWhile and dropWhile operators also take a predicate as their right operand. The operation xs takeWhile p takes the longest prefix of list xs such that every element in the prefix satisfies p. Analogously, the operation xs dropWhile p removes the longest prefix from list xs such that every element in the prefix satisfies p. Here are some examples:
scala> List(1, 2, 3, 4, 5) find (_ <= 0) res41: Option[Int] = None
scala> List(1, 2, 3, -4, 5) takeWhile (_ > 0) res42: List[Int] = List(1, 2, 3)The span method combines takeWhile and dropWhile in one operation, just like splitAt combines take and drop. It returns a pair of two lists, defined by the equality:
scala> words dropWhile (_ startsWith "t") res43: List[java.lang.String] = List(quick, brown, fox)
Like splitAt, span avoids traversing the list xs twice:
scala> List(1, 2, 3, -4, 5) span (_ > 0) res44: (List[Int], List[Int]) = (List(1, 2, 3),List(-4, 5))
The operation xs forall p takes as arguments a list xs and a predicate p. Its result is true if all elements in the list satisfy p. Conversely, the operation xs exists p returns true if there is an element in xs that satisfies the predicate p. For instance, to find out whether a matrix represented as a list of lists has a row with only zeroes as elements:
scala> def hasZeroRow(m: List[List[Int]]) = m exists (row => row forall (_ == 0)) hasZeroRow: (List[List[Int]])Boolean
scala> hasZeroRow(diag3) res45: Boolean = false
Another common kind of operation combines the elements of a list with some operator. For instance:
This is a special instance of a fold operation:
scala> def sum(xs: List[Int]): Int = (0 /: xs) (_ + _) sum: (List[Int])IntSimilarly:
is a special instance of this fold operation:
scala> def product(xs: List[Int]): Int = (1 /: xs) (_ * _) product: (List[Int])IntA fold left operation "(z /: xs) (op)" involves three objects: a start value z, a list xs, and a binary operation op. The result of the fold is op applied between successive elements of the list prefixed by z. For instance:
Or, graphically:
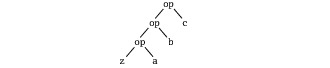
Here's another example that illustrates how /: is used. To concatenate all words in a list of strings with spaces between them and in front, you can write this:
scala> ("" /: words) (_ +" "+ _) res46: java.lang.String = the quick brown foxThis gives an extra space at the beginning. To remove the space, you can use this slight variation:
scala> (words.head /: words.tail) (_ +" "+ _) res47: java.lang.String = the quick brown foxThe /: operator produces left-leaning operation trees (its syntax with the slash rising forward is intended to be a reflection of that). The operator has :\ as an analog that produces right-leaning trees. For instance:
Or, graphically:
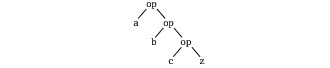
The :\ operator is pronounced fold right. It involves the same three operands as fold left, but the first two appear in reversed order: The first operand is the list to fold, the second is the start value.
For associative operations, fold left and fold right are equivalent, but there might be a difference in efficiency. Consider for instance an operation corresponding to the List.flatten method, which concatenates all elements in a list of lists.[7] This could be implemented with either fold left or fold right:
def flattenLeft[T](xss: List[List[T]]) = (List[T]() /: xss) (_ ::: _)Because list concatenation, xs ::: ys, takes time proportional to its first argument xs, the implementation in terms of fold right in flattenRight is more efficient than the fold left implementation in flattenLeft. The problem is that flattenLeft(xss) copies the first element list xss.head n-1 times, where n is the length of the list xss.
def flattenRight[T](xss: List[List[T]]) = (xss :~List[T]()) (_ ::: _)
Note that both versions of flatten require a type annotation on the empty list that is the start value of the fold. This is due to a limitation in Scala's type inferencer, which fails to infer the correct type of the list automatically. If you try to leave out the annotation, you get the following:
scala> def flattenRight[T](xss: List[List[T]]) = (xss :~List()) (_ ::: _) <console>:15: error: type mismatch; found : List[T] required: List[Nothing] (xss :~List()) (_ ::: _) ^
To find out why the type inferencer goes wrong, you'll need to know about the types of the fold methods and how they are implemented. More on this in Chapter 22. Lastly, although the /: and :\ operators have the advantage that the direction of the slash resembles the graphical depiction of their respective left or right-leaning trees, and the associativity of the colon character places the start value in the same position in the expression as it is in the tree, some may find the resulting code less than intuitive. If you prefer, you can alternatively use the methods named foldLeft and foldRight, which are also defined on class List.
Earlier in the chapter you saw an implementation of method reverse, named rev, whose running time was quadratic in the length of the list to be reversed. Here is now a different implementation of reverse that has linear cost. The idea is to use a fold left operation based on the following scheme:
def reverseLeft[T](xs: List[T]) = (startvalue /: xs)(operation)It only remains to fill in the startvalue and operation parts. In fact, you can try to deduce these parts from some simple examples. To deduce the correct value of startvalue, you can start with the smallest possible list, List(), and calculate as follows:
List() equals (by the properties of reverseLeft)Hence, startvalue must be List(). To deduce the second operand, you can pick the next smallest list as an example case. You know already that startvalue is List(), so you can calculate as follows:
reverseLeft(List()) equals (by the template for reverseLeft)
(startvalue /: List())(operation) equals (by the definition of /:)
startvalue
List(x) equals (by the properties of reverseLeft)Hence, operation(List(), x) equals List(x), which can also be written as x :: List(). This suggests taking as operation the :: operator with its operands exchanged. (This operation is sometimes called "snoc," in reference to ::, which is called cons.) We arrive then at the following implementation for reverseLeft:
reverseLeft(List(x)) equals (by the template for reverseLeft, with startvalue = List())
(List() /: List(x)) (operation) equals (by the definition of /:)
operation(List(), x)
def reverseLeft[T](xs: List[T]) = (List[T]() /: xs) {(ys, y) => y :: ys}(Again, the type annotation in List[T]() is necessary to make the type inferencer work.) If you analyze the complexity of reverseLeft, you'll find that it applies a constant-time operation ("snoc") n times, where n is the length of the argument list. Hence, the complexity of reverseLeft is linear, as hoped for.
The operation xs sort before, where "xs" is a list and "before" is a function that can be used to compare two elements, sorts the elements of list xs. The expression x before y should return true if x should come before y in the intended ordering for the sort. For instance:
scala> List(1, -3, 4, 2, 6) sort (_ < _) res48: List[Int] = List(-3, 1, 2, 4, 6)Note that sort performs a merge sort similar to the msort algorithm shown in the last section, but it is a method of class List whereas msort was defined outside lists.
scala> words sort (_.length > _.length) res49: List[java.lang.String] = List(quick, brown, fox, the)
So far, all operations you have seen in this chapter are implemented as methods of class List, so you invoke them on individual list objects. There are also a number of methods in the globally accessible object scala.List, which is the companion object of class List. Some of these operations are factory methods that create lists. Others are operations that work on lists of some specific shape. Both kinds of methods will be presented in this section.
You've already seen on several occasions list literals such as List(1, 2, 3). There's nothing special about their syntax. A literal like List(1, 2, 3) is simply the application of the object List to the elements 1, 2, 3. That is, it is equivalent to List.apply(1, 2, 3):
scala> List.apply(1, 2, 3) res50: List[Int] = List(1, 2, 3)
The range method, which you saw briefly earlier in the chapter in the discussion of map and flatmap, creates a list consisting of a range of numbers. Its simplest form is List.range(from, until), which creates a list of all numbers starting at from and going up to until minus one. So the end value, until, does not form part of the range.
There's also a version of range that takes a step value as third parameter. This operation will yield list elements that are step values apart, starting at from. The step can be positive or negative:
scala> List.range(1, 5) res51: List[Int] = List(1, 2, 3, 4)
scala> List.range(1, 9, 2) res52: List[Int] = List(1, 3, 5, 7)
scala> List.range(9, 1, -3) res53: List[Int] = List(9, 6, 3)
The make method creates a list consisting of zero or more copies of the same element. It takes two parameters: the length of the list to be created, and the element to be repeated:
scala> List.make(5, 'a') res54: List[Char] = List(a, a, a, a, a)
scala> List.make(3, "hello") res55: List[java.lang.String] = List(hello, hello, hello)
The unzip operation is the inverse of zip. Where zip takes two lists and forms a list of pairs, unzip takes a list of pairs and returns two lists, one consisting of the first element of each pair, the other consisting of the second element:
scala> val zipped = "abcde".toList zip List(1, 2, 3) zipped: List[(Char, Int)] = List((a,1), (b,2), (c,3))
scala> List.unzip(zipped) res56: (List[Char], List[Int]) = (List(a, b, c), List(1, 2, 3))
You might wonder why unzip is a method of the global List object, instead of being a method of class List. The problem is that unzip does not work on any list but only on a list of pairs, whereas Scala's type system requires every method of a class to be available on every instance of that class. Thus, unzip cannot go in the List class. It might be possible to extend Scala's type system in the future so that it accepts methods that only apply to some instances of a class, but so far this has not been done.
The flatten method takes a list of lists and concatenates all element lists of the main list. For example:
scala> val xss = List(List('a', 'b'), List('c'), List('d', 'e')) xss: List[List[Char]] = List(List(a, b), List(c), List(d, e))
scala> List.flatten(xss) res57: List[Char] = List(a, b, c, d, e)
The flatten method is packaged in the global List object for the same reason as unzip: it does not operate on any list, but only on lists with lists as elements, so it can't be a method of the generic List class.
The concat method is similar to flatten in that it concatenates a number of element lists. The element lists are given directly as repeated parameters. The number of lists to be passed to concat is arbitrary:
scala> List.concat(List('a', 'b'), List('c')) res58: List[Char] = List(a, b, c)
scala> List.concat(List(), List('b'), List('c')) res59: List[Char] = List(b, c)
scala> List.concat() res60: List[Nothing] = List()
The map2 method is similar to map, but it takes two lists as arguments together with a function that maps two element values to a result. The function gets applied to corresponding elements of the two lists, and a list is formed from the results:
scala> List.map2(List(10, 20), List(3, 4, 5)) (_ * _) res61: List[Int] = List(30, 80)The exists2 and forall2 methods are similar to exists and forall, respectively, but they also take two lists and a boolean predicate that takes two arguments. The predicate is applied to corresponding arguments:
scala> List.forall2(List("abc", "de"), List(3, 2)) (_.length == _) res62: Boolean = true
scala> List.exists2(List("abc", "de"), List(3, 2)) (_.length != _) res63: Boolean = false
In the next (and final) section of this chapter, we provide insight into Scala's type inference algorithm. You can safely skip the entire section if you're not interested in such details right now, and instead go straight to the conclusion here.
One difference between the previous uses of sort and msort concerns the admissible syntactic forms of the comparison function. Compare:
scala> msort((x: Char, y: Char) => x > y)(abcde) res64: List[Char] = List(e, d, c, b, a)with:
scala> abcde sort (_ > _)
res65: List[Char] = List(e, d, c, b, a)
The two expressions are equivalent, but the first uses a
longer form of comparison function with named parameters and explicit types whereas
the second uses the concise form, (_ > _), where named
parameters are replaced by underscores. Of course, you could
also use the first, longer form of comparison with sort.
However, the short form cannot be used with msort:
scala> msort(_ > _)(abcde) <console>:12: error: missing parameter type for expanded function ((x$1, x$2) => x$1.$greater(x$2)) msort(_ > _)(abcde) ^
To understand why, you need to know some details of Scala's type inference algorithm. Type inference in Scala is flow based. In a method application m(args), the inferencer first checks whether the method m has a known type. If it has, that type is used to infer the expected type of the arguments. For instance, in abcde.sort(_ > _), the type of abcde is List[Char], hence sort is known to be a method that takes an argument of type (Char, Char) => Boolean and produces a result of type List[Char]. Since the parameter types of the function arguments are thus known, they need not be written explicitly. With what it knows about sort, the inferencer can deduce that (_ > _) should expand to ((x: Char, y: Char) => x > y) where x and y are some arbitrary fresh names.
Now consider the second case, msort(_ > _)(abcde). The type of msort is a curried, polymorphic method type that takes an argument of type (T, T) => Boolean to a function from List[T] to List[T] where T is some as-yet unknown type. The msort method needs to be instantiated with a type parameter before it can be applied to its arguments. Because the precise instance type of msort in the application is not yet known, it cannot be used to infer the type of its first argument. The type inferencer changes its strategy in this case; it first type checks method arguments to determine the proper instance type of the method. However, when tasked to type check the short-hand function literal, (_ > _), it fails because it has no information about the types of the implicit function parameters that are indicated by underscores.
One way to resolve the problem is to pass an explicit type parameter to msort, as in:
scala> msort[Char](_ > _)(abcde) res66: List[Char] = List(e, d, c, b, a)Because the correct instance type of msort is now known, it can be used to infer the type of the arguments.
Another possible solution is to rewrite the msort method so that its parameters are swapped:
def msortSwapped[T](xs: List[T])(less: (T, T) => Boolean): List[T] = {Now type inference would succeed:
// same implementation as msort, // but with arguments swapped }
scala> msortSwapped(abcde)(_ > _)
res67: List[Char] = List(e, d, c, b, a)
What has happened is that the inferencer used the known type of
the first parameter abcde to determine the type
parameter of msortSwapped. Once the precise type of msortSwapped was known,
it could be used in turn to infer the type of the second parameter, (_ > _).
Generally, when tasked to infer the type parameters of a polymorphic method, the type inferencer consults the types of all value arguments in the first parameter list but no arguments beyond that. Since msortSwapped is a curried method with two parameter lists, the second argument (i.e., the function value) did not need to be consulted to determine the type parameter of the method.
This inference scheme suggests the following library design principle: When designing a polymorphic method that takes some non-function arguments and a function argument, place the function argument last in a curried parameter list by its own. That way, the method's correct instance type can be inferred from the non-function arguments, and that type can in turn be used to type check the function argument. The net effect is that users of the method will be able to give less type information and write function literals in more compact ways.
Now to the more complicated case of a fold operation. Why is there the need for an explicit type parameter in an expression like the body of the flattenRight method shown previously?
(xss :~List[T]()) (_ ::: _)
The type of the fold-right operation is polymorphic in two type variables.
Given an expression:
(xs :~z) (op)The type of xs must be a list of some arbitrary type A, say xs: List[A]. The start value z can be of some other type B. The operation op must then take two arguments of type A and B and must return a result of type B, i.e., op: (A, B) => B. Because the type of z is not related to the type of the list xs, type inference has no context information for z. Now consider the erroneous expression in the method flattenRight above:
(xss :~List()) (_ ::: _) // this won't compileThe start value z in this fold is an empty list, List(), so without additional type information its type is inferred to be a List[Nothing]. Hence, the inferencer will infer that the B type of the fold is List[Nothing]. Therefore, the operation (_ ::: _) of the fold is expected to be of the following type:
(List[T], List[Nothing]) => List[Nothing]This is indeed a possible type for the operation in that fold but it is not a very useful one! It says that the operation always takes an empty list as second argument and always produces an empty list as result. In other words, the type inference settled too early on a type for List(), it should have waited until it had seen the type of the operation op. So the (otherwise very useful) rule to only consider the first argument section in a curried method application for determining the method's type is at the root of the problem here. On the other hand, even if that rule were relaxed, the inferencer still could not come up with a type for op because its parameter types are not given. Hence, there is a Catch-22 situation which can only be resolved by an explicit type annotation from the programmer.
This example highlights some limitations of the local, flow-based type inference scheme of Scala. It is not present in the more global Hindley-Milner style of type inference used in functional languages such as ML or Haskell. However, Scala's local type inference deals much more gracefully with object-oriented subtyping than the Hindley-Milner style does. Fortunately, the limitations show up only in some corner cases, and are usually easily fixed by adding an explicit type annotation.
Adding type annotations is also a useful debugging technique when you get confused by type error messages related to polymorphic methods. If you are unsure what caused a particular type error, just add some type arguments or other type annotations, which you think are correct. Then you should be able to quickly see where the real problem is.
Now you have seen many ways to work with lists. You have seen the basic operations like head and tail, the first-order operations like reverse, the higher-order operations like map, and the utility methods in the List object. Along the way, you learned a bit about how Scala's type inference works.
Lists are a real work horse in Scala, so you will benefit from knowing how to use them. For that reason, this chapter has delved deeply into how to use lists. Lists are just one kind of collection that Scala supports, however. The next chapter is broad, rather than deep, and shows you how to use a variety of Scala's collection types.
[1] For a graphical depiction of the structure of a List, see Figure 22.2 here.
[2] Chapter 19 gives more details on covariance and other kinds of variance.
[3] Type parameters will be explained in more detail in Chapter 19.
[4] As mentioned in Section 10.12, the term pair is an informal name for Tuple2.
[5] This is class scala.StringBuilder, not java.lang.StringBuilder.
[6] By higher-order operators, we mean higher-order functions used in operator notation. As mentioned in Section 9.1, higher-order functions are functions that take other functions as parameters.
[7] List.flatten will be explained in the next section of this chapter.